Bài 7: Thuật toán Q-Learning

Ta sẽ tìm hiểu về các phương pháp đưa ra lời giải bằng cách tìm ra hàm hành động-giá trị tối ưu $Q^{\ast}$. Ưu điểm của hàm hành động-giá trị so với hàm giá trị là nó chứa thêm thông tin về đánh giá các hành động, vì vậy, có thể vừa tận dụng để đưa ra chính sách. Ý tưởng là nếu chúng ta có $Q_k$ gần với $Q^{\ast}$ thì chính sách tham lam theo $Q_k$ sẽ gần với chính sách tối ưu. Thuật toán đầu tiên được giới thiệu trong bài viết này là thuật toán Q-Learning.

Thuật toán Q-Learning

Ta xét một bộ chuyển vị, bao gồm: $(X_t, A_t, R_t, Y_{t+1})$. Ta xét các đại lượng sau:

\[\delta_{t+1}(Q) = R_{t+1}+\gamma\max_{b\in\mathcal{A}}Q(Y_{t+1}, b)-Q(X_t, A_t)\] \[Q_{t+1}(x, a) = Q_t(x, a) +\alpha_t\delta_{t+1}(Q)\mathbb{I_{x=X_t,a=A_t}}, \forall x, a\in\mathcal{X}\times\mathcal{A}\]

Ở bộ chuyển vị trên, ta xét $Y_{t+1}$ thay vì $X_{t+1}$ để tổng quát hóa. Bạn đọc còn nhớ về khái niệm on-policy và off-policy, nếu như $Y_{t+1}\neq X_{t+1}$, nghĩa là sự chuyển vị trạng thái trong quá trình học khác với quá trình đưa ra hành động thì được gọi là off-policy. Ngược lại, nếu chúng ta sử dụng học online trong quá trình cập nhật từng bước, ta có: $X_{t+1}=Y_{t+1}$ và tất nhiên nó được gọi là on-policy. Chú ý rằng, Q-Learning là off-policy. Lý do bởi đại lượng:

\[\max_{b\in\mathcal{A}}Q(Y_{t+1}, b)\]

Được tính toán dựa trên so sánh toàn bộ các hành động $b$ nên trạng thái $Y_{t+1}$ phải được sinh từ một tập mẫu. Ở bài sau, ta sẽ được so sánh với một thuật toán on-policy để bạn đọc có thể hình dung thêm về vấn đề này.

Thuật toán này có nét tương đồng với TD(0) và cũng được lý thuyết chứng minh rằng sẽ hội tụ tới $Q^{\ast}$ trong một số điều kiện nhất định, dưới đây là mã giả cập nhật thuật toán Q-Learning:

Hình 1: Thuật toán Q-Learning

Thuật toán Deep Q-Learning

Đối với không gian trạng thái $\mathcal{X}$ vô hạn, ta tiến hành xấp xỉ $Q$ dưới dạng: $Q_{\theta}$. Trong phần này, ta sẽ tìm hiểu một thuật toán gây tiếng vang vào thời điểm nó được công bố năm 2015 là thuật toán Deep Q-Learning. Deep Q-Learning được xây dựng dựa trên ý tưởng của thuật toán Q-Learning nhưng sử dụng các mô hình học sâu để xấp xỉ hàm $Q$ (các tham số mô hình học sâu này chính là $\theta$).

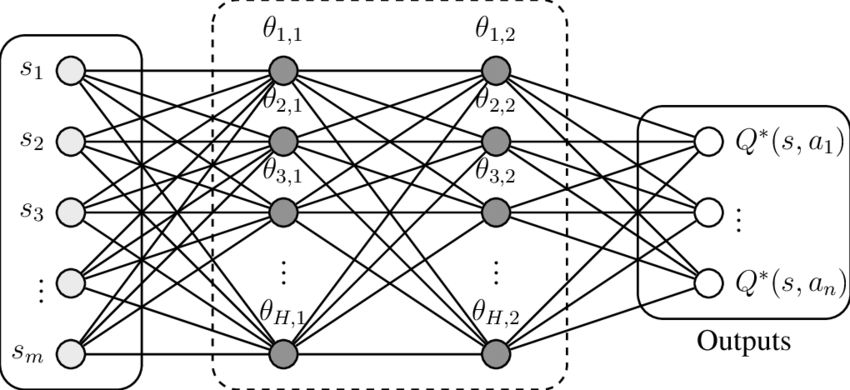
Hình 2: Mô hình Q-Network

Q-Network chính là mạng dùng để xấp xỉ, mạng này có đầu vào là một vector có $n$ chiều (có thể là $\mathbb{R^n}$, …). Mạng này có đầu ra hữu hạn, mỗi đầu ra $a% sẽ thể hiện giá trị hàm $Q(x, a)$ tương ứng với $x$ là vector input. Trong Deep Q-Learning, có 3 thành phần quan trọng như sau:

• Replay Memory
• Policy Network
• Target Network

Replay Memory đơn giản là một cấu trúc dữ liệu để lưu trữ các bộ chuyển vị trong quá trình tương tác với môi trường. Điều này là dễ hiểu, bởi Q-Learning là off-policy nên việc học diễn ra trên các mẫu đã được thu thập trước đó. Mỗi lần học, Replay Memory sẽ tiến hành sinh ra một batch, batch này sẽ được cập nhật vào mạng Q-Network dựa vào hàm mất mát với đại lượng mất mát chính là $\delta$ trong Q-Learning:

\[\delta = Q(x, a) - (r+\gamma\max_{a}Q(y, a)), (1)\]

Tương ứng với mỗi lần ta chuyển vị từ $x$ sang $y$ bằng hành động $a$ trong batch huấn luyện. Ta có thể lựa chọn các hàm mất mát như trong học sâu, ví dụ như: Huber loss, MSE, …

Trong Deep Q-Learning có hai mạng được sử dụng là Policy Network và Target Network. Mục đích chính của của Policy Network là đưa ra hành động (với bài báo ban đầu, tác giả sử dụng cơ chế đưa ra hành động là $\epsilon$-greedy trên hàm $Q$). Mục đích của Target Network là duy trì một đại lượng xấp xỉ với giá trị thực của hàm $Q$. Một điều lưu ý trong công thức $(1)$ là dựa vào sự chênh lệch của $Q(x, a)$ và $(r+\gamma\max_{a}Q(y, a))$, trong đó, policy network là mạng sinh ra đại lượng đầu tiên $Q(x, a)$, còn target network là mạng sinh ra đại lượng thứ hai $(r+\gamma\max_{a}Q(y, a))$. Target Network được cập nhật sau một số chuowng theo Policy Network, trong khi đó, Policy Network được cập nhật mỗi batch.

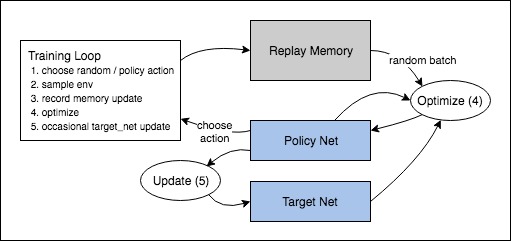
Hình 3: Sơ đồ thuật toán Deep Q-Learning

Hình 4: Mã giả thuật toán Deep Q-Learning