Bài 6: Giới thiệu về bài toán điều khiển (Control)
Như vậy, ta đã làm quen với một bài toán lớn trong học tăng cường là bài toán dự đoán giá trị, bây giờ, ta sẽ xem xét một bài toán lớn còn lại trong học tăng cường, đó là bài toán điều khiển. Bài toán điều khiển có mục tiêu là học chính sách tối ưu $\pi^{\ast}$. Trong bài toán Multi-armed bandits, thực chất, ta cũng đã giải quyết bài toán này; các thuật toán mà blog đã trình bày bao gồm $\epsilon$-greedy và gradient bandit. Ta sẽ cùng nhau phân tích kỹ hơn về bài toán điều khiển trong học tăng cường.
Các dạng bài toán học trong học tăng cường
Trong học tăng cường, các phương pháp học thường được chia thành 2 loại chính, đó là:
- Có tương tác: Trong phương pháp học này được chia làm hai loại:
- Online learning.
- Active learning.
- Không tương tác: Trong quá trình học, tác tử không tương tác thêm với môi trường.
Thông thường, các giải thuật học tăng cường thường được xem ở dạng có tương tác và là Online learning. Ta sẽ có một số bàn luận về các phương pháp còn lại.
Đầu tiên là học không tương tác, phương pháp này còn được gọi là batch learning. Một ví dụ đó là một tác tử tương tác đủ nhiều với môi trường và sinh ra được một tập mẫu về hành động, trạng thái. Tác tử sẽ tiến hành học dựa trên tập mẫu đã thu thập được trong quá trình tương tác đã và không tương tác thêm gì với môi trường trong suốt quá trình học. Trong phương pháp này, có thể thấy rằng, các hành động trong tập mẫu đã được chọn sẵn nên tác tử phải xây dựng thuật toán theo hướng off-policy (nhắc lại, đó là khi chính sách đưa ra hành động khác với chính sách đang học).
Tiếp theo là active learning. Tương tự giống với học không tương tác, tác tử sẽ cố gắng học một chính sách tối ưu dựa trên một tập mẫu tương tác với môi trường trước đó. Điểm khác của active learning là nó có thể tương tác với môi trường thêm để có thể học được chính sách tốt nhất có thể. Có rất ít tài liệu lý thuyết về active learning được sử dụng trong MDP, mặc dù trên thực tế, active learning được sử dụng khá nhiều. Trong blog này, ta sẽ quan tâm tới các phương pháp online learning.
Thuật toán UCB
Thuật toán này là thuật toán cải tiến của $\epsilon$-greedy. $\epsilon$-greedy như ta đã biết thì lựa chọn hành động dựa trên tham lam và ý tưởng của UCB cũng dựa trên tham lam. Ta gọi đại lượng $U_t(a)$ là khoảng tin cậy của hành động $a$ tại thời điểm $t$ như sau:
\[U_t(a) = r_t(a)+c\sqrt{\frac{2\log t}{n_t(a)}}\]Trong đó, $n_t(a)$ là số lần hành động $a$ được lựa chọn trước thời điểm $t$, $r_t(a)$ là phần thưởng trung bình của hành động $a$ trước thời điểm $t$. Một hành động có UCB lớn hơn nếu nó có ít thông tin về nó, điều này sẽ khuyến khích tác tử khai phá hành động đó. Hằng số $c$ có tác dụng để kiểm soát sự khai phá. Tại mỗi thời điểm, ta đơn giản chỉ lựa chọn hành động mang lại UCB lớn nhất, ta có thể xem cài đặt thuật toán như sau:
class Agent:
def __init__(self, fair: Fair):
self.reward_at_machine = [0 for i in range(fair.length)]
self.value_function = [0 for i in range(fair.length)]
self.trial_times = [0.000000001 for i in range(fair.length)] # Tránh việc chia cho 0
self.trials = 2
self.fair = fair
self.action_length = fair.length
self.c = 0.01
def choose_action(self):
tmp = 0
machine = 0
for i in range(self.action_length):
if self.reward_at_machine[i] + self.c * np.sqrt(np.log(self.trials)/(self.trial_times[i])) > tmp:
tmp = self.reward_at_machine[i] + self.c * np.sqrt(np.log(self.trials)/(self.trial_times[i]))
machine = i
self.trials += 1
self.trial_times[machine] += 1
reward = self.fair.pull_at_machine(machine)
self.reward_at_machine[machine] = (self.reward_at_machine[machine] * (self.trial_times[machine] - 1) + reward) / self.trial_times[machine]
return reward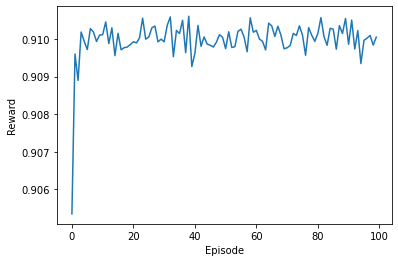
Hình 1: Kết quả thuật toán UCB
Thuật toán UCRL2
Ta sẽ tìm hiểu một kỹ thuật mới trong bài toán điều khiển, đó là tối thiểu hóa regret - đây là đại lượng thể hiện sự chênh lệch giữa tổng phần thưởng của chính sách tối ưu với tổng phần thưởng nhận được trong quá trình học.
Ta xét trường hợp MDP của chúng ta là unichain. Một chuỗi MDP được gọi là unichain nếu như với mọi chính sách sinh ra chuỗi hành động thì đều kết thúc bởi một chuỗi các trạng thái lặp lại. Ta gọi:
\[\rho^{\pi}(x) = \lim\dfrac{1}{N}\mathbb{E}[\sum_{t=0}^{N-1}R_{t+1} \| X_0 = x]\]Vì tính chất của chuỗi Markov là unichain, tức là cuối cùng đều kết thúc bởi một chuỗi các trạng thái lặp lại nên:
\[\rho^{\pi}(x) = \rho^{\pi}(x') = \rho^{\pi}, \forall x, x'\in\mathcal{X}\]Và cũng bởi vì chuỗi trạng thái sau cùng sẽ lặp lại nên mỗi trạng thái $x$ dưới một chính sách $\pi$ đều có một phân phối xác suất là $\mu_{\pi}(x)$, ta có:
\[\rho^{\pi} =\sum_{x\in\mathcal{X}} \mu_{\pi}(x)r(x, \pi(x))\]Ta gọi $\rho^{\ast}=\max\rho^{\pi}$, khi đó, ta định nghĩa đại lượng sau được gọi là reget:
\[\mathbf{R_T^{\mathbf{A}}} = T\rho^{\ast}-\mathcal{R_T^{\mathbf{A}}}\]Chú ý $T$ ở đây là một số thời điểm, không phải phép biến đổi Bellman. $\mathcal{R_T^{\mathbf{A}}} = \sum_{t=0}^{T-1}R_{t+1}$. Tối thiểu hóa regret tương đương với tối đa hóa tổng phần thưởng nhận được. Trong phương trình trên, $\mathbf{A}$ là thuật toán học. Một thuật toán học có tên là UCRL2(1/(3T)) được chứng minh là đạt được regret theo hàm logarit. Dưới đây là mã giả của thuật toán UCRL2:
- Pha đầu tiên định nghĩa một tập các chuỗi MDP: $\mathcal{C_t}$. Tại mỗi thời điểm, tác tử sẽ tương tác với các đại lượng $n_2’, n_3’$ để ghi lại số lượng hành động theo một chính sách ${\pi_t}^{\ast}$. Tập $\mathcal{C_t}$ này càng về sau sẽ càng được tăng cường số bước để học: ($n_2:=n_2+n_2’, n_3:=n_3+n_3’$).
Hình 2: Pha 1 của thuật toán UCRL2
- Tiếp theo, một giải thuật $\texttt{OPTSOLVE}$ (dựa trên ý tưởng của UCB) được sử dụng để giải quyết pha 2 đó là tìm chính sách ${\pi_t}^{\ast}$ và mô hình $\mathcal{M_t}^{\ast}$ tối ưu tại mỗi mô hình tăng cường, giải thuật này lặp cho tới khi:

Hình 2: Pha 2 của thuật toán UCRL2
Bên cạnh các phương pháp đã đề cập, bạn đọc có thể tìm hiểu thêm về các thuật toán khác như: PAC-MDP, MORMAX, MBIE, …
