Bài 5: Các thuật toán giải bài toán dự đoán giá trị

Bây giờ, ta sẽ tìm hiểu thêm về các thuật toán khác bên cạnh Value Iteration để giải quyết bài toán dự đoán giá trị. Ta vẫn sẽ xét trường hợp MDP có hữu hạn trạng thái, nghĩa là $\mathcal{A}$ hữu hạn. Bài viết này sẽ tìm hiểu về thuật toán Temporal Difference cổ điển, Every-visit Monte-Carlo và cuối cùng là sự kết hợp của cả hai thuật toán này.

Thuật toán Temporal Difference TD(0)

Xét một chuỗi MRP. Dãy hàm $\hat{V_0}(x), \hat{V_1}(x), \dots,$ thể hiện ước lượng của $V^{\pi}(x)$ tại các thời điểm. Ta có công thức cập nhật trong thuật toán Temporal Difference như sau:

\[\delta_{t+1}=R_{t+1} +\gamma \hat{V_{t}}(X_{t+1}) - \hat{V_t}(X_t)\] \[\hat{V}_{t+1}(X_t) = \hat{V_{t}}(X_t) + \alpha_t\times\delta_{t+1}\]

Trong đó, $\alpha_t$ được gọi là dãy step-size. Thông thường, $\alpha_t$ được chọn thỏa mãn điều kiện Robbins-Monro:

\[\sum_{t=0}^{+\infty}\alpha_t=+\infty; \sum_{t=0}^{+\infty}\alpha_t^2 < +\infty, (1)\]

Ta sẽ trình bày hai vấn đề quan trọng của thuật toán này: Thứ nhất, làm thế nào để biết rằng thuật toán này sẽ hội tụ? Thứ hai, nếu nó hội tụ, liệu nó có hội tụ tới giá trị $V^{\pi}$ cần ước lượng hay không?

Ta sẽ xem xét vào câu hỏi thứ hai trước, nếu $\hat{V_t}$ hội tụ về một hàm giá trị $\hat{V}$, liệu ta có suy ra $\hat{V}=V^{\pi}$ hay không? Nhắc lại về $T^{\pi}$, ta có, trong chuỗi MRP định nghĩa bởi một chính sách cố định thì:

\[(T^{\pi}\hat{V})(x) = r(x, \pi(x)) + \gamma\times\sum_{y\in\mathcal{X}}\mathcal{P}(y,R | x, \pi(x))\times \hat{V}(y), \forall x\in\mathcal{X}\]

Ta có: $X_{t+1}$ là trạng thái kế tiếp của $X_t$ theo chính sách $\pi$ và phần thưởng sinh ra trong quá trình chuyển vị này là $R_{t+1}$, do đó, ta hoàn toàn có thể viết được:

\[(T^{\pi}\hat{V})(X_t) = \mathbb{E}[R_{t+1} + \gamma\times \hat{V}(X_{t+1})]\]

Suy ra được:

\[(T^{\pi}\hat{V})(X_t) - \hat{V}(X_t) = \mathbb{E}[R_{t+1} + \gamma\times \hat{V}(X_{t+1}) - \hat{V}(X_t)]\]

Do đó, nếu $\hat{V_t}$ hội tụ về một hàm giá trị $\hat{V}$ thì $\delta\rightarrow 0$, điều này, có nghĩa là $\hat{V}$ là nghiệm của phương trình:

\[T^{\pi}V=V\]

Phương trình này được chứng minh là có nghiệm duy nhất trong một số trường hợp, chính vì vậy, dưới một số điều kiện, ta có thể khẳng định được $\hat{V}=V^{\pi}$. Bạn đọc có thể đọc thêm ở cái tài liệu tham khảo để xem chứng minh nghiệm duy nhất của phương trình.

Bây giờ, câu hỏi thứ nhất, đó là liệu thuật toán của chúng ta có hội tụ về một điểm $\hat{V}$ hay không là một câu hỏi khó hơn. Bài viết chỉ giới thiệu cho bạn đọc rằng một số trường hợp thì thuật toán của chúng ta sẽ hội tụ về $\hat{V_t}$. Trường hợp mà người ta vẫn hay áp dụng trong thực tế đó là dựa vào điều kiện $(1)$. Về lý thuyết, người ta có thể chọn $\alpha_t = ct^{-\eta}$ để đảm bảo điều kiện hội tụ ($1/2<\eta\leq 1$). Tuy nhiên, trong thực tế, người ta thường dùng step-size là hằng số. Như đã trình bày, các định lý chứng minh này chỉ chứng minh dưới một số điều kiện, chứ không phải toàn bộ không gian thực. Đối với câu hỏi thứ nhất, bạn đọc cần có kiến thức về phương trình vi phân thường (ODE) để có thể đọc hiểu được chứng minh.

Hình 1: Thuật toán Temporal Difference

Thuật toán Every-visit Monte-Carlo

Thuật toán Temporal Difference cập nhật từng thời điểm, ta sẽ tìm hiểu một thuật toán cập nhật tại nhiều thời điể. Xét bài toán MRP của ta có tính chương hồi (episodic). Ta gọi $T_k, k=0,1,\dots$ là thời điểm mà các chương thứ $k=0,1,\dots$ tương ứng kết thúc. Như đã trình bày ở bài 3, khi một trạng thái kết thúc đạt được thì sẽ không thể thay đổi được trạng thái nữa, vì vậy, phân phối xác xuất $\mathcal{P}$ được khởi tạo lại sau mỗi chương. Ta xét tổng phần thưởng tích lũy suy biến như sau:

\[\mathcal{R_{t}} = \sum_{s=t}^{T_{k(t)+1}-1}\gamma^{s-t}R_{s+1}\]

$\mathcal{R_{t}}$ cho biết tổng phần thưởng tích lũy bắt đầu từ $s=t$ và cho tới khi đạt được trạng thái kết thúc $s=T_{k(t)+1}$. Ta có: $V(x) = \mathbb{E}[\mathcal{R_t} | X_t =x]$. Ta tiến hành cập nhật $\hat{V_t}$ như sau:

\[\hat{V_{t+1}}(x) = \hat{V_{t}}(x) + \alpha_t(\mathcal{R_{t}} - \hat{V_{t}}(x))\mathbb{I_{X_t=x}}, \forall x\in\mathcal{X}\]

$\mathbb{I}$ là hàm nhận giá trị bằng $1$ nếu điều kiện đúng, bằng $0$ nếu điều kiện sai. Chính vì sự xuất hiện của $\mathcal{R_{t}}$ đòi hỏi cần phải có thông tin của cả chuỗi chuyển vị ($R_t, R_{t+1},\dots, R_{T_{k(t)+1}}$) trong một chương, các thuật toán giải theo hướng cập nhật theo một chương như vậy được gọi là multi-step. Thuật toán này cũng được chứng minh là hội tụ và sẽ hội tụ về $V^{\pi}$ dưới một số điều kiện. Dưới đây là mã giả của thuật toán:

Hình 2: Thuật toán Every-visit Monte-Carlo

So sánh thuật toán Temporal Difference và Monte-Carlo

Ta sẽ so sánh hai thuật toán này và chỉ ra ưu, nhược điểm của hai thuật toán bằng cách xem xét một ví dụ sau:

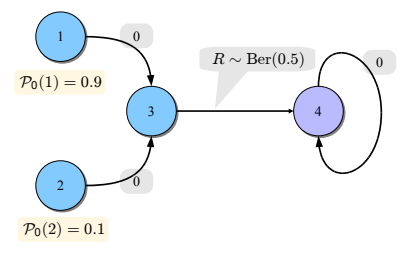
Hình 3: Ví dụ minh họa về một bài toán MDP

Ta có một bài toán MDP đơn giản, và bởi vì ở từng trạng thái, ta chỉ có duy nhất một cách có thể chuyển trạng thái nên đây có thể xem là MRP; ngoài ra ta thấy rằng, trạng thái $4$ là trạng thái kết thúc.

• Đối với trường hợp của bài toán: Temporal Difference (TD(0)) sẽ cho hội tụ nhanh hơn. Xét $10k$ chương, mỗi chương bao gồm việc chuyển vị trạng thái từ $1$ hoặc $2$ (tùy vào việc ngẫu nhiên trạng thái ban đầu) tới trạng thái $4$. Bằng phân phối xác suất, trong $10k$ chương này, trung bình sẽ có $k$ chương xuất phát từ $2$; cả $10k$ chương này đều phải chuyển vị qua trạng thái $3$. Ta giả sử rằng $\alpha_t=\frac{1}{t+1}$. Khi đó, theo công thức cập nhật của TD(0) thì $|V_{10k}(3) - V_{10k-1}(3)|\approx O(\frac{1}{10k})$, suy ra rằng, độ chính xác của $\hat{V}(2)$ cũng tăng dần theo $k$. Một mặt, theo thuật toán Monte-Carlo, trong $10k$ chương này, $\hat{V}(2)$ được cập nhật $k$ lần theo các chương. Ta thấy rằng, trong tổng tích lũy phần thưởng của một chương, chỉ có phần thưởng $R$ được sinh ra từ chuyển vị từ trạng thái $3$ sang $4$ theo phân phối xác suất $\text{Ber}(0.5)$ (bạn đọc có thể kiểm chứng được $\text{Var}(\text{Ber}(0.5)) = 0.5\times (1-0.5) = 0.25$) nên: $\text{Var}(\mathcal{R_t}) = 0.25$ tại mọi chương, không giảm khi $k$ tăng dần. Bởi lẽ vậy, $\hat{V}(2)$ sẽ hội tụ chậm hơn và kết quả là Monte-Carlo sẽ chậm hơn.
• Bây giờ, ta xét trường hợp khi thay phân phối xác suất $\text{Ber}(0.5)$ thành $1$. Khi đó, $\mathcal{R_t}=1$ là giá trị thực (hiển nhiên phương sai bằng 0). Do đó, $\hat{V}(2)$ hội tụ rất nhanh theo từng chương. Một mặt, $\hat{V}(2)$ hội tụ không ảnh hưởng bởi $\hat{V}(3)$; đây chính là điểm yếu của thuật toán TD(0) do $\hat{V}(2)$ hội tụ yêu cầu $\hat{V}(3)$ phải hội tụ trước. Vì lẽ đó, trong trường hợp này Monte-Carlo sẽ nhanh hơn.

Thuật toán TD($\lambda$)

Như vậy, có thể thấy rằng, cả thuật toán TD(0) và Monte-Carlo đều có ưu điểm của riêng nó, nên một ý tưởng khá tự nhiên đó là kết hợp cả hai thuật toán này, đó là khi thuật toán TD($\lambda$) được ra đời. Ta sẽ xét tổng phần thưởng tích lũy trong một chương nhưng với độ dài thay đổi $k$:

\[\mathcal{R_{t:k}} = \sum_{s=t}^{t+k}\gamma^{s-t}R_{s+1} + \gamma^{k+1}\times\hat{V_t}(X_{t+k+1})\]

Bạn đọc có thể bước đầu cảm nhận được đại lượng này là sự kết hợp của cả TD(0) và Monte-Carlo: thành phần đầu thể hiện tổng phần thưởng tích lũy sau $k$ thời điểm, thành phần thứ hai thể hiện đánh giá truy hồi theo hàm giá trị. Ta dùng đại lượng này để tiến hành cập nhật ước lượng cho $\hat{V_t}(x)$. Ta tiến hành cập nhật theo công thức sau:

\[\delta_{t+1}=R_{t+1}+\gamma\hat{V_t}(X_{t+1})-\hat{V_t}(X_{t})\] \[z_{t+1} (x)=\mathbb{I_{x=X_t}} + \gamma\lambda z_t(x), \forall x\in\mathcal{X}\] \[\hat{V_{t+1}}(x) = \hat{V_{t}}(x) +\alpha_t\delta_{t+1}z_{t+1}(x), \forall x\in\mathcal{X}\] \[z_0(x) = 0, \forall x\in\mathcal{X}\]

Trong đó, $\lambda$ là siêu tham số, khi $\lambda=0$, thuật toán trên trở thành TD(0), còn khi $\lambda =1$, bạn đọc có thể kiểm chứng rằng thuật toán trên chính là Monte-Carlo. Đại lượng $z$ được gọi là eligibility trace.Dưới đây là mã giả của thuật toán:

Hình 4: Thuật toán TD($\lambda$)