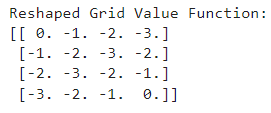Bài 4: Giới thiệu về bài toán dự đoán giá trị (Value prediction)
Như vậy, qua 3 bài viết đầu tiên, những khái niệm cơ bản về học tăng cường đã được trình bày, ngoài ra, một bài toán ví dụ mở đầu về học tăng cường cũng đã được nêu và bắt đầu từ bài viết này, ta sẽ xem xét vào những khía cạnh sâu hơn của học tăng cường. Bài viết này sẽ giới thiệu về bài toán dự đoán giá trị (value prediction problems). Nhắc lại khái niệm của MRP: Khi nói đến MRP là ta đang xem xét MDP gán với một chính sách cụ thể $\pi$ nào đó. Và bài toán dự đoán giá trị rất đơn giản, đó là chúng ta cần phải ước lượng được hàm $V^{\pi}$.
Phép biến đổi Bellman
Xét trường hợp chính sách $\pi$ cố định. Ta gọi $T^{\pi}: \mathbb{R}^{\mathcal{X}}\rightarrow\mathbb{R}^{\mathcal{X}}$ là phép biến đổi Bellman gán với chính sách $\pi$, cụ thể như sau:
\[(T^{\pi}V)(x) = r(x, \pi(x)) + \gamma\times\sum_{y\in\mathcal{X}}\mathcal{P}(y,R \| x, \pi(x))\times V(y), \forall x\in\mathcal{X}\]Phương trình Bellman ở bài 2 đã cho ta biết rằng: $V^{\pi}(x) = r(x, \pi(x)) + \gamma\times\sum_{y\in\mathcal{X}}\mathcal{P}(y,R | x, \pi(x))\times V^{\pi}(y), \forall x\in\mathcal{X}$, do đó, nói cách khác, ta phải có đẳng thức sau:
\[T^{\pi}V^{\pi} = V^{\pi}\]Một cách tương tự, ta định nghĩa phép biến đổi Bellman tối ưu như sau:
\[(T^{\ast}V)(x) = \sup_{a\in\mathcal{A}} \{r(x, \pi(x)) + \gamma\times\sum_{y\in\mathcal{X}}\mathcal{P}(y,R \| x, \pi(x))\times V^{\pi}(y), \} \forall x\in\mathcal{X}\]Và ta cũng có từ kết quả bài 2 rằng: $T^{\ast}V^{\ast}=V^{\ast}$. Ta sẽ đi phân tích ý nghĩa của $T^{\pi}$ và $T^{\ast}$:
- Dựa vào $T^{\pi}$, ta có thể cài đặt các thuật toán quy hoạch động để tính chính xác được $V^{\pi}$, qua đó, ta sẽ biết được rằng giá trị ứng với chính sách $\pi$ có tốt hay không.
- Còn đối với $T^{\ast}$, rõ ràng, chúng ta không thể “quy hoạch động” để tìm $V^{\ast}$ dựa vào $V^{\ast}$, tuy nhiên, người ta đã chứng minh được lý thuyết rằng việc áp dụng phép biến đổi tối ưu Bellman sẽ hội tụ về được $V^{\ast}$ dưới một số điều kiện nhất định - phần tiếp theo sẽ trình bày kỹ hơn về phần này. Vậy, ta có thể hiểu rằng $T^{\ast}$ được ứng dụng để tìm giá hàm giá trị tại chính sách tối ưu.
Trước khi trình bày phần tiếp theo, mục này sẽ khép lại bằng mối quan hệ của $T, V$ với $Q$, ta có:
\[T^{\pi}Q(x, a) = r(x, a) + \gamma\times\sum_{y\in\mathcal{X}}\mathcal{P}(y,R \| x, a)\times Q(y, \pi(y)), \forall x, a\in\mathcal{X}\times\mathcal{A}\] \[T^{\ast}Q(x, a) = r(x, a) + \gamma\times\sum_{y\in\mathcal{X}}\mathcal{P}(y,R \| x, a)\times \sup_{b\in\mathcal{A}} Q(y, b), \forall x, a\in\mathcal{X}\times\mathcal{A}\]Phương pháp value iteration (quy hoạch động xấp xỉ)
Xét dãy hàm giá trị khởi đầu bằng giá trị của $V_0$ bất kỳ, các phần tử tiếp theo được tính bằng công thức truy hồi như sau:
\[V_{k+1} = T^{\ast} V_k, \forall k\geq 0\]Định lý Banach fixed-point chứng minh được dãy hàm này sẽ hội tụ về $V^{\ast}$. Một cách tương tự, bằng cách xét dãy hàm:
\[Q_{k+1} = T^{\ast} Q_k, \forall k\geq 0, (1)\]Ta cũng sẽ thu được dãy hàm hội tụ đến giá trị $Q^{\ast}$. Như vậy, có thể thấy rằng các phương pháp này cho ta xấp xỉ được các giá trị tối ưu $V^{\ast}, Q^{\ast}$, bởi lẽ đó, người ta còn hay gọi các phương pháp này là quy hoạch động xấp xỉ.
Bên cạnh ý nghĩa tìm ra giá trị tối ưu tại từng trạng thái, phương pháp value iteration này còn là tiền đề cho một số phương pháp Policy Iteration. Ta gọi $\pi$ là chính sách tham lam tương ứng với $Q$, khi đó, ta có kết quả của một chứng minh bởi Singh et al. như sau:
\[V^{\pi}(x) \geq V^{\ast}(x)-\dfrac{2}{1-\gamma} \| Q^{\pi}-Q^{\ast} \|, \forall x\in\mathcal{X}\]Trong đó, chuẩn được sử dụng ở trên là chuẩn L1. Định lý này cho ta biết rằng, nếu ta càng làm giảm được $Q^{\pi}$ về giá trị tối ưu $Q^{\ast}$ thì chính sách của ta thu được làm cho hàm giá trị càng gần được về tối ưu. Chính vì vậy, ở trong bước cập nhật $(1)$, nếu ta gọi $\pi_k$ là chính sách tham lam tương ứng với $Q_k$ cập nhật theo từng bước thì từ định lý trên ta sẽ có $V^{\pi_k}(x)$ hội tụ về $V^{\ast}$. Bài toán dự đoán giá trị không giải quyết việc đưa ra cơ chế lựa chọn hành động mà chỉ đi ước lượng giá trị, do đó, muốn giải được các bài toán học tăng cường, cần phải định nghĩa thêm về các cơ chế đưa ra hành động. Bài toán này được gọi là bài toán điều khiển, sẽ được trình bày ở các bài sau, còn hiện tại, ta tiếp tục đi sâu vào phân tích bài toán dự đoán giá trị.
Thuật toán Value Iteration được trình bày ngắn gọn như sau:
Hình 1: Thuật toán Value Iteration
Dự đoán giá trị trong bài toán GridWorld
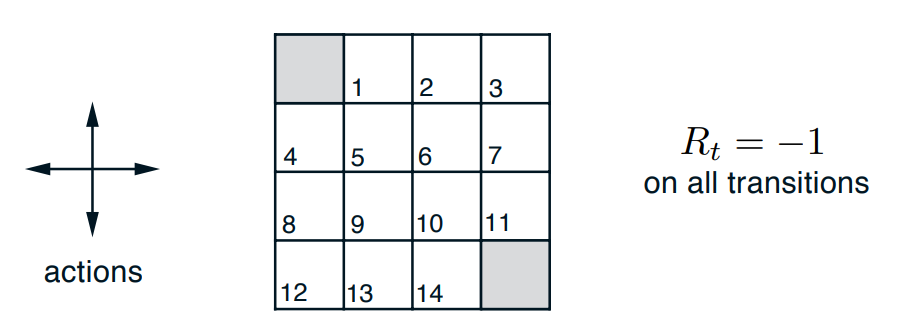
$\texttt{OpenAI}$ là một thư viện open-source rất nổi tiếng về các bài toán học tăng cường, trong ví dụ này, ta sẽ tìm hiểu cách để sử dụng mã nguồn của OpenAI tạo ra một môi trường bài toán GridWorld. Chúng ta xét một bài toán GridWorld $4\times 4$ cụ thể như sau (các trường hợp kích cỡ lớn hơn được xem xét hoàn toàn tương tự):
Hình 2: Ví dụ minh họa về GridWorld
Chúng ta có tập trạng thái $\mathcal{S} = {1,2,\dots, 14}$ biểu diễn $14$ trạng thái không phải trạng thái kết thúc, $2$ ô ở góc trái trên cùng và góc phải dưới cùng là hai trạng thái kết thúc. Tại mỗi trạng thái, ta có tập hành động $\mathcal{A} = {1, 2, 3, 4}$ đại diện cho các hướng di chuyển: Bắc, Nam, Đông, Tây, ứng với mỗi hành động, ta chỉ được di chuyển 1 ô. Tất cả các phần thưởng thu được đều là $-1$, tại trạng thái kết thúc, ta định nghĩa phần thưởng là $0$ và kết thúc chương. Đây là bài toán có chương và xét trường hợp $\gamma = 1$, nghĩa là phần thưởng của chúng ta không bị suy biến. Khi đó, theo bài 2, ta có:
\[V^{\ast}(x) = \mathbb{E}[ \sum_{t=0}^{+\infty}\gamma^t R_{t+1} \| X_0 = x] = \mathbb{E}[\sum_{t=0}^{T_x-1} R_{t+1} \| X_0 = x]\]Trong đó, $X_{T_x}$ là trạng thái kết thúc nếu ban đầu chúng ta xuất phát từ $x$. Ta có thể thấy rằng $X_0\rightarrow X_1\rightarrow\dots\rightarrow X_{T_x}$ chính là quãng đường ngắt nhất mà từ $x$ có thể đi đến 1 trong 2 trạng thái kết thúc. Như vậy, ta có thể viết lại được:
\[V^{\ast}(x) = \mathbb{E}[\sum_{t=0}^{T_x-1} -1 \| X_0 = x] = -T_x\]Trong đó, $T_x$ chính là số ô ngắn nhất cần phải đi từ $x$ đến 1 trong 2 trạng thái kết thúc. Nhờ nhận xét này, ta có thể tính toán được giá trị tối ưu tại các trạng thái như sau:
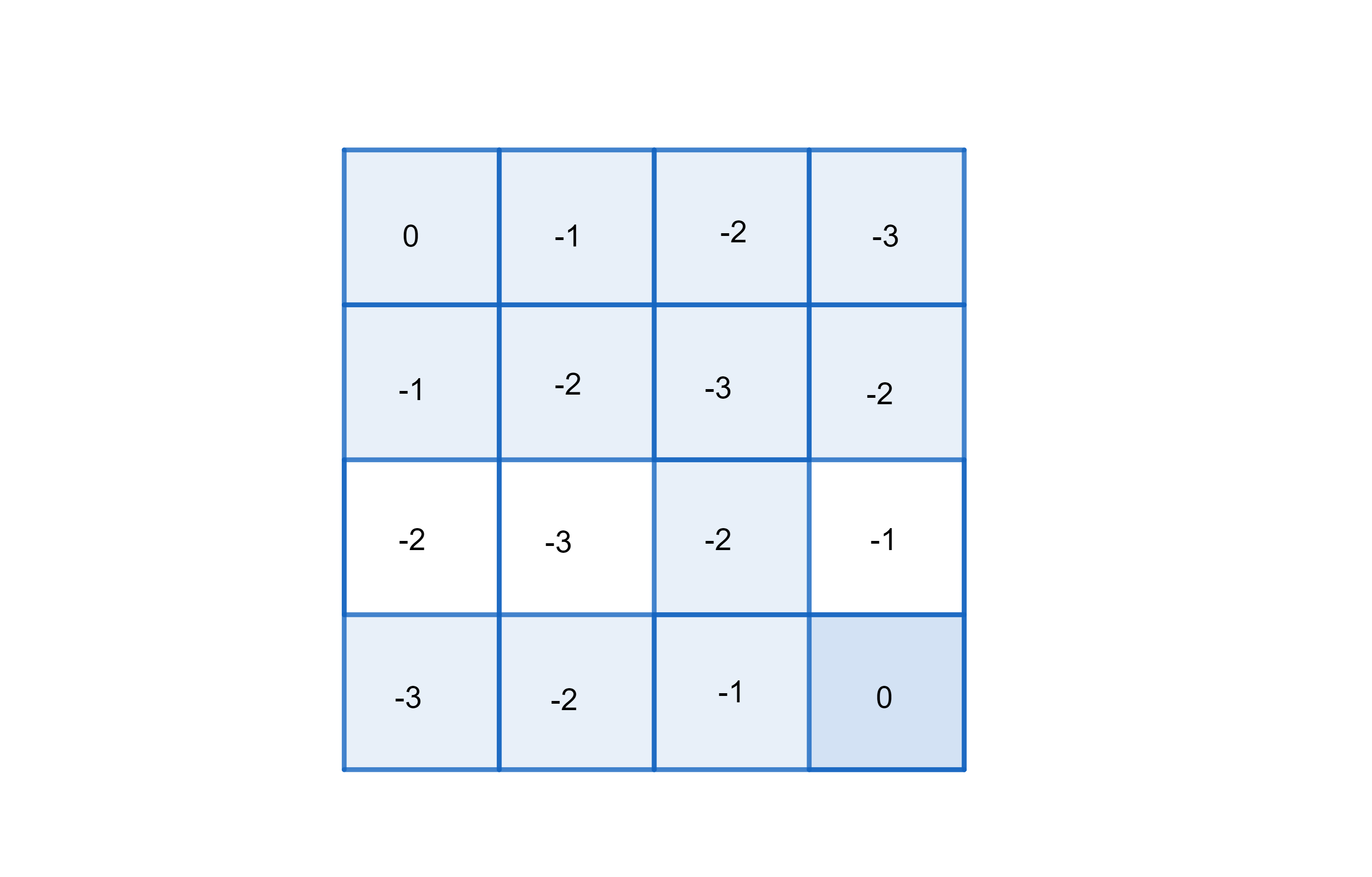
Hình 3: Hàm giá trị tối ưu của bài toán
Bây giờ, ta sẽ kiểm chứng điều này bằng thuật toán Value Iteration. Đầu tiên, ta sẽ khởi tạo bài toán GridWorld bằng cách sử dụng thư viện $\texttt{gym}$:
import io
import numpy as np
import sys
from gym.envs.toy_text import discrete
UP = 0
RIGHT = 1
DOWN = 2
LEFT = 3
class GridworldEnv(discrete.DiscreteEnv):
metadata = {'render.modes': ['human', 'ansi']}
def __init__(self, shape=[4,4]):
self.shape = shape
nS = np.prod(shape)
nA = 4
MAX_Y = shape[0]
MAX_X = shape[1]
P = {}
grid = np.arange(nS).reshape(shape)
it = np.nditer(grid, flags=['multi_index'])
while not it.finished:
s = it.iterindex
y, x = it.multi_index
# P[s][a] = (prob, next_state, reward, is_done)
P[s] = {a : [] for a in range(nA)}
is_done = lambda s: s == 0 or s == (nS - 1)
reward = 0.0 if is_done(s) else -1.0
# Terminal state
if is_done(s):
P[s][UP] = [(1.0, s, reward, True)]
P[s][RIGHT] = [(1.0, s, reward, True)]
P[s][DOWN] = [(1.0, s, reward, True)]
P[s][LEFT] = [(1.0, s, reward, True)]
# Not a terminal state
else:
ns_up = s if y == 0 else s - MAX_X
ns_right = s if x == (MAX_X - 1) else s + 1
ns_down = s if y == (MAX_Y - 1) else s + MAX_X
ns_left = s if x == 0 else s - 1
P[s][UP] = [(1.0, ns_up, reward, is_done(ns_up))]
P[s][RIGHT] = [(1.0, ns_right, reward, is_done(ns_right))]
P[s][DOWN] = [(1.0, ns_down, reward, is_done(ns_down))]
P[s][LEFT] = [(1.0, ns_left, reward, is_done(ns_left))]
it.iternext()
# Initial state distribution is uniform
isd = np.ones(nS) / nS
# We expose the model of the environment for educational purposes
# This should not be used in any model-free learning algorithm
self.P = P
super(GridworldEnv, self).__init__(nS, nA, P, isd)Tiếp theo, ta cài đặt thuật toán Value Iteration, chính sách lựa chọn hành động ở đây tuân theo chiến lược tham lam:
def value_iteration(env, theta=0.0001, discount_factor=1.0):
def one_step_lookahead(state, V):
A = np.zeros(env.nA)
for a in range(env.nA):
for prob, next_state, reward, done in env.P[state][a]:
A[a] += prob * (reward + discount_factor * V[next_state])
return A
V = np.zeros(env.nS)
while True:
# Stopping condition
delta = 0
# Update each state...
for s in range(env.nS):
# Do a one-step lookahead to find the best action
A = one_step_lookahead(s, V)
best_action_value = np.max(A)
# Calculate delta across all states seen so far
delta = max(delta, np.abs(best_action_value - V[s]))
V[s] = best_action_value
# Check if we can stop
if delta < theta:
break
# Create a deterministic policy using the optimal value function
policy = np.zeros([env.nS, env.nA])
for s in range(env.nS):
# One step lookahead to find the best action for this state
A = one_step_lookahead(s, V)
best_action = np.argmax(A)
# Always take the best action
policy[s, best_action] = 1.0
return policy, V
Hình 4: Kết quả thu được bằng thuật toán Value Iteration
Như vậy, có thể thấy rằng, thuật toán đã chạy ra kết quả chính xác với những gì ta phân tích.