Bài 3: Bài toán Multi-armed bandits
Đầu tiên, ta sẽ xem xét một bài toán được gọi là “Hello world” đối với lĩnh vực học tăng cường, đó là bài toán “Multi-armed bandits”. Ta xét môi trường trong trường hợp đơn giản nhất, đó là môi trường chỉ có duy nhất một trạng thái, và bất cứ hành động nào thực hiện với môi trường cũng làm môi trường không thay đổi trạng thái. Đối với môi trường như vậy, thì ta chỉ quan tâm tới tập hành động; mục tiêu chính của ta là tìm xem hành động nào đem lại tổng phần thưởng mong đợi lớn nhất. Đây cũng chính là bài toán “Multi-armed bandits”. Trong bài toán này, tác tử là chúng ta, môi trường là một không gian (giả sử là casino) bao gồm các máy đánh bạc (slot machine). Ta cần phải có chiến thuật sao cho phần thưởng ta thu được thì quán casino này là lớn nhất.

Hình 1: Minh họa về Máy đánh bạc
Trên hình là minh họa về một Máy đánh bạc, là một thành phần của môi trường mà ta tương tác. Máy đánh bạc đơn giản chỉ có 1 tay kéo (pull arm), mỗi lần chơi, ta đơn giản chỉ cần kéo cái tay đó và sẽ nhận được phần thưởng theo một luật cụ thể. Trong phạm vi bài viết này, ta không quan tâm tới luật đó, mà ta chỉ quan tâm tới các yếu tố toán học mô hình bài toán này. Ta giả sử rằng, phần thưởng mà ta nhận được từ mỗi lần kéo là tuân theo một phân phối xác suất nào đó. Ta sẽ mô hình hóa cụ thể bài toán dưới đây.
Bây giờ tưởng tượng ta có $k$ máy đánh bạc tại casino. Không gian hành động của chúng ta là $\mathcal{A} = { 1,2,\dots, k}$, trong đó, hành động $i$ thể hiện rằng ta sẽ tới máy đánh bạc thứ $i$ và thực hiện kéo cái tay của máy đó. Mỗi máy thứ $i$ sẽ có một phân phối xác suất về phần thưởng $R{\sim}P_i$ khác nhau. Ví dụ, ta có thể hiểu $P_i = \mathcal{N}(\mu_i,\,\sigma_i^{2})$, tuy nhiên thực tế, các phân phối xác suất này có thể không phải chỉ là phân phối chuẩn. Tại mỗi bước $t=0,1,\dots$, ta chọn hành động $A_t\in\mathcal{A}$ sẽ thu được phần thưởng $R_t$ sinh ra từ phân phối xác suất $P_{A_t}$. Nhiệm vụ của chúng ta là phải có một chính sách để có thể thu được tổng phần thưởng kỳ vọng tối đa.
Phân tích bài toán
Ta thấy rằng: $r(x, a) = \mathbb{E}[R_{(x, a)}]$, và vì không gian trạng thái của chúng ta chỉ có duy nhất một trạng thái nên $x$ cố định, nên thực tế:
\[r(x, a) = \mathbb{E}[R_{(x, a)}] = \mathbb{E}[P_a]\]Vậy, hiển nhiên rằng, nếu $\mathbb{E}[P_{a^{\ast}}] = \max_{a\in\mathcal{A}}\mathbb{E}[P_a]$ thì ta chỉ việc luôn chọn $a^{\ast}$ để luôn thu được tổng phần thưởng kỳ vọng tối đa.
Như vậy, phải chăng bài toán này chỉ đơn giản là tìm kỳ vọng của các xác suất đầu vào $P_i$ rồi so sánh chọn kỳ vọng lớn nhất? Không, bài toán trong học tăng cường không đơn giản như vậy. Như đã đề cập phần trước, $P_i$ thậm chí không phải là những phân phối xác suất mà chúng ta biết và thực tế là ta cũng khó có thể mô hình hóa được mà chỉ tính toán ước lượng qua các phương pháp xác suất thống kê. Hơn nữa, kể cả môi trường của chúng ta xác định được $P_i$ nhưng không có nghĩa tác tử của chúng ta biết được $P_i$, nó phải học phân phối này qua các tương tác với môi trường. Tới đây, có hai khái niệm quan trọng của học tăng cường được xem xét và cũng đã đề cập ở bài đầu tiên, đó là khai phá (exploration) và tận dụng (exploitation).
Ta sẽ nói về tận dụng trước, tận dụng đơn giản là dựa vào những tri thức mà ta biết về môi trường để đưa ra được quyết định tốt nhất. Trong ngữ cảnh này, chính là việc nếu ta ước lượng được các $\widetilde{P_i}\approx P_i$ thì ta sẽ chọn hành động $a^{\ast} = \text{argmax}_{a\in\mathcal{A}} \mathbb{E}[\widetilde{P_a}]$ (như đã phân tích ở trước).
Tiếp theo, ta sẽ nói đến khai phá, một câu hỏi tưởng chừng là đơn giản nhưng không dễ để trả lời, đó là làm thế nào để chúng ta biết được máy đánh bạc nào sẽ đưa ra phần thưởng lớn nhất? Rõ ràng, nếu chỉ chơi 1 lần ở hai máy $C$ và $D$, giả sử tổng phần thưởng thu được ở $C$ là $15$, ở $D$ là $10$, ta so sánh $15>10$ rồi vội vàng đi đến kết luận máy $C$ sẽ đem lại phần thưởng tốt hơn máy $D$. Cách làm như vậy là chưa đủ căn cứ, lý do bởi phần thưởng được sinh ra bởi một phân phối xác suất. Trong một lần sinh xác suất bởi hai phân phối $P_C, P_D$ thì kể cả trong trường hợp kỳ vọng của $P_C$ có lớn hơn $P_D$ nhưng vẫn có thể xảy ra trường hợp giá trị sinh ra bởi $P_C$ thấp hơn $P_D$. Như vậy, bên cạnh tận dụng, ta cần phải có một chiến thuật để khai phá không gian trạng thái, hành động.
Cả tận dụng và khai phá đều là hai khái niệm quan trọng trong học tăng cường, và có thể nói là chúng trade-off lẫn nhau. Một giải thuật học tăng cường luôn phải đảm bảo 2 yếu tố này và phải xem xét kỹ lưỡng trong quá trình thiết kế giải thuật.
Tạo một test case cho bài toán
Đây là phần đầu tiên trong toàn bộ blog sẽ trình bày chi tiết về lập trình một bài toán Học tăng cường cũng như một phương pháp để giải bài toán. Đầu tiên, chúng ta cần khởi tạo không gian về trạng thái, hành động của bài toán (vì trạng thái là bất biến trong bài toán Multi-armed bandits nên ta chỉ quan tâm tới các hành động)
class Arm:
def __init__(self, probability: float, deviation: float):
self.probability = probability
self.deviation = deviation
self.positive_reward = 1
self.negative_reward = 0
def pull(self) -> int:
return self.positive_reward * np.random.normal(self.probability, self.deviation)Xét một trường hợp đơn giản, khi ta có: $P_i=\mathcal{N}(\mu_i,\,\sigma_i^{2})$. Lớp Arm sẽ trừu tượng hóa các máy đánh bạc bằng cách lưu các thông tin về phân phối xác suất; ngoài ra, lớp này cung cấp một phương thức pull để có thể nhận được phần thưởng. Tiếp theo, ta định nghĩa về quán casino qua một lớp là Fair, lớp này là tập hợp của các máy đánh bạc:
class Fair:
def __init__(self):
self.arms = []
self.length = 0
def add_arm(self, arm: Arm):
self.arms.append(arm)
self.length += 1
def pull_at_machine(self, index: int) -> int:
try:
return self.arms[index].pull()
except:
print("Error at Fair.pull_at_machine")
raiseCuối cùng, ta tạo ví dụ một bài toán cụ thể như sau:
f = Fair()
f.add_arm(Arm(0.7, 0.01))
f.add_arm(Arm(0.8, 0.01))
f.add_arm(Arm(0.6, 0.01))
f.add_arm(Arm(0.5, 0.03))
f.add_arm(Arm(0.7, 0.02))
f.add_arm(Arm(0.7, 0.01))
f.add_arm(Arm(0.8, 0.01))
f.add_arm(Arm(0.6, 0.03))
f.add_arm(Arm(0.5, 0.05))
f.add_arm(Arm(0.7, 0.02))
f.add_arm(Arm(0.7, 0.03))
f.add_arm(Arm(0.8, 0.06))
f.add_arm(Arm(0.6, 0.01))
f.add_arm(Arm(0.5, 0.01))
f.add_arm(Arm(0.9, 0.01))
f.add_arm(Arm(0.7, 0.01))
f.add_arm(Arm(0.91, 0.01))
f.add_arm(Arm(0.6, 0.02))
f.add_arm(Arm(0.5, 0.04))
f.add_arm(Arm(0.7, 0.05))Như vậy, ta đặt chú ý nhất vào arm thứ 17, arm mà có giá trị kỳ vọng là 0.91, đây cũng sẽ là phân phối xác suất mà ta cần tìm ra.
Thuật toán epsilon-greedy
Bây giờ, ta sẽ xem xét một giải thuật cũng được coi là “Hello world” đối với học tăng cường, đó là thuật toán $\epsilon$-greedy. Giải thuật này rất đơn giản. Ta gọi $Q_t(a)$ là đại lượng thể hiện phần thưởng trung bình của hành động $a$ được chọn trước thời điểm $t$ và $A_t$ là hành động chọn tại thời điểm $t$. Tại mỗi thời điểm $t$ ta chọn tham lam $A_t = \text{argmax} ( Q_{t}(a) | a\in\mathcal{A} )$. Ta sẽ cân bằng việc tận dụng này bằng chiến lược khai phá như sau: Cố định $\epsilon$ là một ngưỡng. Tại mỗi thời điểm, ta sẽ lựa chọn ngẫu nhiên một hành động với xác suất $\epsilon$, và chọn tham lam với xác suất $1-\epsilon$. Sau khi chọn xong hành động $A_t$ ta sẽ thu được phần thưởng $R_{t+1}$, ta tiến hành cập nhật lại $Q_t(A_t)$ theo $Q_{t-1}(A_t)$ và $R_t$, công thức cập nhật này có thể tham khảo ở đoạn mã sau đây:
class Agent:
def __init__(self, fair: Fair):
self.reward_at_machine = [0 for i in range(fair.length)]
self.trial_times = [0 for i in range(fair.length)]
self.fair = fair
self.epsilon = 0.01
self.action_length = fair.length
def choose_action(self):
if random.random() < self.epsilon:
machine = random.randint(0, self.action_length - 1)
else:
machine = self.reward_at_machine.index(max(self.reward_at_machine))
self.trial_times[machine] += 1
reward = self.fair.pull_at_machine(machine)
self.reward_at_machine[machine] = (self.reward_at_machine[machine] *
(self.trial_times[machine]-1)+reward)/ \
self.trial_times[machine]
return reward
def drive(self, num_episodes: int, num_timesteps_per_episode: int):
rewards = []
for episode in range(num_episodes):
reward = 0
for timestep in range(num_timesteps_per_episode):
reward += self.choose_action()
rewards.append(reward / num_timesteps_per_episode)
return rewardsTrong mã nguồn trên $\texttt{self.reward_at_machine}$ chính là hàm $Q_t(a)$ mà ta đề cập, bạn đọc có thể dễ dàng kiểm chứng công thức cập nhật của $Q_t(a)$. Trong đoạn mã trên, có một khái niệm quan trọng chưa được đề cập tới trong blog này, đó là chương/hồi (episode). Đây cũng là một khái niệm quan trọng khác trong học tăng cường. Đối với các bài toán học tăng cường, việc mô hình hóa về MDP thường gặp phải tình huống tác tử không thể thay đổi trạng thái của môi trường nữa; ví dụ, trong bài toán robotic để tự học cách di chuyển, tới 1 lúc nào đó, robot sẽ rơi vào trạng thái ‘deadlock’, nghĩa là không thể thay đổi trạng thái được nữa.
Hoặc ví dụ như trong video trên, cánh tay robot đã rơi vào ‘deadlock’ và không thể nào dịch chuyển tới điểm cần tới nữa. Ta gọi những trường hợp như vậy là trạng thái kết thúc (terminal state). Hiểu một cách đơn giản hơn, trạng thái kết thúc là trạng thái mà ở đó tác tử không thể thay đổi được trạng thái nữa. Và ngay khi thời điểm ở trạng thái kết thúc, tác tử sẽ được gọi là hoàn thành một chương (episode). Thông thường, các bài toán học tăng cường sẽ phân làm các chương và đánh giá tổng phần thưởng mong đợi suy biến trong chương đó. Trong bài toán Multi-armed bandits này, ta giả sử rằng sau một số những thời điểm cố định thì chương đó mặc định sẽ kết thúc. Dưới đây là kết quả thu được bằng thuật toán $\epsilon$-greedy:
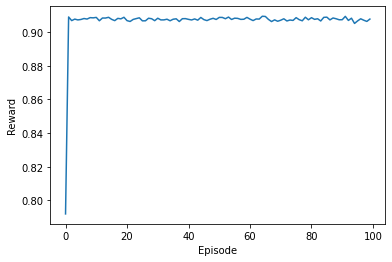
Hình 2: Kết quả của thuật toán epsilon-greedy
Như vậy, quay trở lại khi ta sinh test case, ta đã nói rằng 0.91 chính là kỳ vọng phần thưởng lớn nhất mà các máy đánh bạc có thể cung cấp cho ta và quả thực, thuật toán $\epsilon$-greedy đã tìm ra được giá trị kỳ vọng này. Hơn thế, thực nghiệm của tác giả còn cho thấy, trong 10000 lần thực hiện kéo tay thì máy số 17 được kéo tới 8442 lần, chiếm 84,42% số lần chọn hành động. Tỉ lệ còn lại được chia đều các máy còn lại, do cơ chế của chọn hành động ngẫu nhiên theo tỉ lệ $\epsilon$. Bạn đọc có thể tự cài đặt lại thuật toán với các điều chỉnh của mình để có thể kiểm chứng điều này.
Thuật toán gradient bandit
Thuật toán $\epsilon$-greedy là thuật toán lựa chọn hành động dựa trên ước lượng hàm hành động-giá trị. Các thuật toán đưa ra hành động dựa trên các hàm giá trị cũng như hành động-giá trị được gọi là các thuật toán value-based. Bây giờ, ta sẽ tìm hiểu một thuật toán policy-based để giải bài toán này. Thay vì ta ước lượng hành động đem lại giá trị lớn nhất, ta sẽ tính toán phân phối xác suất hành động cho bài toán (hay chính là khái niệm chính sách ngẫu nhiên mà bài trước ta nhắc tới).
Với mỗi hành động $a\in\mathcal{A}$, ta gọi $H_t(a)$ tại thời điểm $t$ là giá trị ưu tiên đối với hành động $a$, mục tiêu của ta rất đơn giản: hành động càng tốt thì có giá trị ưu tiên càng cao và ngược lại. Khi đó, chính sách ngẫu nhiên mà ta dùng để chọn hành động như sau:
\[\pi_t(a) = \text{Pr}(A_t=a)=\dfrac{e^{H_t(a)}}{\sum_{b\in\mathcal{A}} H_t(b)}\]Ta sử dụng hàm softmax để có thể đưa ra hành động, đối với các bạn đã quen với những giải thuật học máy, học sâu thì việc đưa qua một hàm softmax để lấy phân phối xác suất là điều quen thuộc. Trong bài toán Multi-armed bandits thì ta muốn làm tối đa mục tiêu sau: $\mathbb{E}[R_t]$ tại mỗi thời điểm $t$. Như vậy, ta đưa về một bài toán tìm cực đại của một đại lượng phụ thuộc vào $\pi_t(a)$. Nếu như đối với các bài toán trong học máy thông thường, ta cần phải tìm cực tiểu của một hàm mất mát thì trong học tăng cường, ta thường phải tìm cực đại của tổng phần thưởng kỳ vọng. Đối với các bài toán tìm cực tiểu, ta dùng gradient descent; còn với các bài toán tìm cực đại, ta dùng gradient ascent. Bài viết này chỉ muốn đề cập tới ý tưởng của phương pháp gradient bandit, bạn đọc có thể tìm thêm ở tài liệu tham khảo để xem chứng minh về công thức $\frac{\partial \mathbb{E}[R_t]}{\partial H_t(a)}$ ở các tài liệu tham khảo. Từ công thức tính gradient đó, ta có công thức cập nhật như sau:
\[H_{t+1}(A_t) = H_t(A_t) + \alpha\times(R_t-\overline{R_t})(1-\pi_t(A_t))\] \[H_{t+1}(a) = H_t(a) - \alpha\times(R_t-\overline{R_t})\pi_t(a), \forall a\neq A_t\]Trong đó, $\alpha$ hay được gọi là các hằng số học (learning rate). Ta có triển khai của thuật toán này như sau:
# Gradient bandit
class Agent:
def __init__(self, fair: Fair):
self.H = np.ones(fair.length)
self.trial_times = 0
self.fair = fair
self.action_length = fair.length
self.total_reward = 0
self.alpha = 0.01
def choose_action(self):
def softmax(H):
h = H - np.max(H)
exp = np.exp(h)
return exp / np.sum(exp)
# Choose action
policy = softmax(self.H)
machine = int(np.random.choice(self.action_length, p=policy))
reward = self.fair.pull_at_machine(machine)
# Update H by gradient ascent
self.total_reward += reward
self.trial_times += 1
avg_reward = self.total_reward / self.trial_times
tmp = self.H[machine] + self.alpha*(reward-avg_reward)*(1-policy[machine])
self.H -= self.alpha*(reward-avg_reward)*policy
self.H[machine] = tmp
return reward
def drive(self, num_episodes: int, num_timesteps_per_episode: int):
rewards = []
for episode in range(num_episodes):
reward = 0
for timestep in range(num_timesteps_per_episode):
reward += self.choose_action()
rewards.append(reward / num_timesteps_per_episode)
return rewardsDưới đây là kết quả đạt được bởi thuật toán Gradient Bandit:
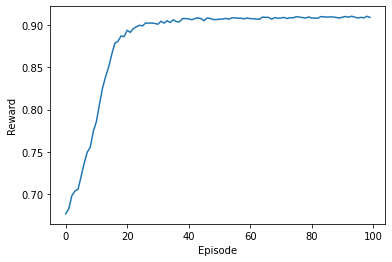
Hình 3: Kết quả của thuật toán gradient bandit
Bên cạnh $\epsilon$-greedy và gradient bandit, còn rất nhiều thuật toán cổ điển để giải quyết bài toán Multi-armed bandits, bạn đọc có thể tìm hiểu cũng như triển khai các thuật toán như UCB, Boltzmann, … Bài viết hy vọng đã cung cấp cho bạn đọc một góc nhìn khởi đầu về các bài toán học tăng cường cũng như các thuật toán để giải quyết chúng, hy vọng bạn đọc cảm thấy đỡ bỡ ngỡ hơn khi đọc các tài liệu về học tăng cường.