Trong bài viết thứ hai này, mình sẽ giới thiệu về Chuỗi đưa quyết định Markov (Markov decision process). Phần đầu tiên trình bày về các khái niệm cơ bản trong MDP và các phần còn lại sẽ trình bày về các khái niệm quan trọng khác trong bài toán học tăng cường, đó là hàm giá trị (value function) và hàm hành động-giá trị (action-value function).

Chuỗi đưa quyết định Markov

Một chuỗi Markov thường được biểu diễn bởi bộ ba $\mathcal{M} = (\mathcal{X}, \mathcal{A}, \mathcal{P})$. Trong đó $\mathcal{X}$ là tập không gian trạng thái, $\mathcal{A}$ là tập không gian hành động. Phân phối xác suất $\mathcal{P}$ được gọi là phân phối xác suất chuyển trạng thái. Một MDP được gọi là hữu hạn nếu cả $\mathcal{X}$ và $\mathcal{A}$ đều hữu hạn.

Giả sử, trạng thái hiện tại của môi trường là $x$, tác tử của chúng ta chọn một hành động là $a$. Khi đó: $\mathcal{P}(y, R | x, a)$ sẽ cho ta biết xác suất mà trạng thái của môi trường là $y$ và phần thưởng mà tác tử nhận được trong sự chuyển dịch này là $R$. Ta có thể thấy rằng: $\mathcal{P}(\cdot | x, a)$ là một ánh xạ: $\mathcal{X}\times\mathbb{R}\rightarrow\mathbb{R}$. Thông thường, phân phối xác suất chuyển trạng thái là ẩn với tác tử, nghĩa là tác tử không thể nào biết được phân phối xác suất trạng thái môi trường nếu nó thực hiện hành động $a$ tại trạng thái $x$. Trong bài toán điều khiển, nếu tác tử cố gắng học biểu diễn phân phối xác suất này bằng một phương pháp xấp xỉ nào đó, ta gọi đó là model-based, ngược lại, nếu tác tử không dựa vào học biểu diễn này, thì ta gọi đó là model-free. Các phương pháp dựa trên model-free thường chạy nhanh hơn, tuy nhiên, độ chính xác không bằng được model-based. Ta sẽ xem xét chi tiết hơn về phần này ở các bài sau.

Phần thưởng chính là một đại lượng để ước lượng xem rằng hành động vừa chọn có tốt hay không và tốt hay không ra sao. Phần thưởng càng lớn thì hành động vừa đưa ra càng tốt, càng nhỏ thì hành động đưa ra càng tệ. Như đã trình bày ở phần trước, ta có: $(y, R){\sim}\mathcal{P}(\cdot | x, a)$. Mỗi giá trị $R_{(x,a)}$ được sinh ra ở từng bước chuyển vị được gọi là phần thưởng tức khắc (immediate reward). Ta định nghĩa thêm đại lượng quan trọng sau:

\[r(x, a) = \mathbb{E}[R_{(x, a)}]\]

Đại lượng này được gọi là phần thưởng kỳ vọng. Dễ thấy, phần thưởng kỳ vọng là một ánh xạ $r: \mathcal{X}\times\mathcal{A}\rightarrow\mathbb{R}$.

Bây giờ, ta sẽ xem xét chuỗi Markov theo thời gian, lý do bởi sự tương tác giữa tác tử với môi trường diễn ra theo chương, hồi. Ta gọi $t$ là bước thời gian hiện tại của chuỗi, gọi $X_t\in\mathcal{X}$ là trạng thái hiện tại của môi trường, $A_t\in\mathcal{A}$ là hành động được lựa chọn.

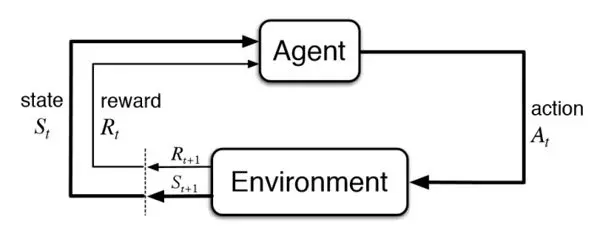
Hình 1: Minh họa về Học tăng cường

Sau khi thực hiện hành động, môi trường sẽ chuyển dịch trạng thái theo phân phối: $(X_{t+1}, R_{t+1}) {\sim} \mathcal{P}(\cdot | x, a)$. Ta có thể thấy rằng, sự tương tác giữa tác tử và môi trường theo thời gian có thể biểu diễn được thành: $X_0, A_0, R_1, X_1, A_1, R_2, X_2, \dots$ và trong học tăng cường, mục tiêu của chúng ta là tìm ra các hành động $A_t$ để phần thưởng của tác tử ở từng thời điểm là lớn nhất. Tất nhiên, khái niệm phần thưởng ở từng thời điểm là lớn nhất là rất mơ hồ, có hai yếu tố như sau: thứ nhất, phần thưởng sinh ra ở từng thời điểm tuân theo một phân phối xác suất, nên một hành động tốt đôi khi không đem lại phần thưởng tức khắc tốt hơn một hành động tồi; thứ hai, sau khi lựa chọn xong một hành động thì trạng thái môi trường bị thay đổi và ta không biết chắc chắn rằng liệu trạng thái môi trường thay đổi này có tệ hơn hay tốt hơn trạng thái môi trường nếu chúng ta lựa chọn một hành động khác hay không. Vì vậy, để có thể giải bài toán MDP một cách chặt chẽ, mục tiêu của chúng ta là tối đa hóa tổng phần thưởng kỳ vọng suy biến (expected total discounted reward).Ta gọi đại lượng sau là giá trị trả về (return):

\[\mathcal{R} = \sum_{t=0}^{+\infty}\gamma^t R_{t+1}\]

Trong đó, $\gamma$ được gọi là hệ số suy biến (discount factor). Mục tiêu của bài toán học tăng cường chính là tối đa hóa $\mathbb{E}[\mathcal{R}]$, đây cũng chính là cùng một đại lượng thể hiện bởi hai tên gọi khác nhau: tổng phần thưởng kỳ vọng suy biến và kỳ vọng giá trị trả về (expected return) - hai khái niệm này cũng sẽ được dùng luân phiên trong blog này nhưng người đọc cần biết được đại lượng mà cả hai khái niệm này muốn đề cập. Như vậy, lời giải của bài toán MDP chính là đưa ra một cơ chế hành động làm cực đại hóa tổng phần thưởng kỳ vọng suy biến, khi đó, cơ chế này được gọi là tối ưu.

Hàm giá trị (value function)

Cách đầu tiên mà để giải bất kỳ bài toán nào là duyệt toàn bộ. Ta có thể liệt kê ra toàn bộ các cơ chế đưa ra hành động để tìm ra cơ chế tốt nhất. Tất nhiên rằng, không gian của các cơ chế này rất lớn và thậm chí là không đếm được nhưng ta cứ giả sử rằng, ta có thể liệt kê được, khi đó, một câu hỏi tự nhiên mà ta sẽ đặt ra là: làm thế nào để biết cơ chế A tốt hơn cơ chế B? Khi đó, ta có thể dựa vào tính toán trên mô hình MDP để so sánh tổng phần thưởng kỳ vọng suy biến nhận được của hai cơ chế. Tuy nhiên, cách này rõ ràng là không khả thi, và có một phương pháp tốt hơn để có thể làm được điều này, đó là tính toán hàm giá trị (value function).

Ta gọi $V^{\ast}(x)$, với $x\in\mathcal{X}$ là tổng phần thưởng kỳ vọng suy biến tối ưu nếu ta thực hiện chuỗi Markov bắt đầu từ trạng thái $x$. Khi đó: $V^{\ast}:\mathcal{X}\rightarrow\mathbb{R}$ được gọi là giá trị tối ưu. Một cơ chế đưa ra hành động mà đạt được giá trị tối ưu tại tất cả các trạng thái thuộc $\mathcal{X}$ được gọi là tối ưu.

Tiếp theo, ta sẽ mô hình hóa cơ chế đưa ra hành động. Tên gọi phù hợp hơn cho khái niệm này là chính sách (policy) và sẽ được sử dụng xuyên suốt blog bắt đầu từ đây. Thông thường có hai loại chính sách:

Chính sách cố định

Chính sách cố định là một ánh xạ trực tiếp $\pi: \mathcal{X}\rightarrow\mathcal{A}$, thể hiện rằng, với bất kỳ $t\geq 0$ nào thì ta luôn có: $A_t$ được chọn trực tiếp dựa vào $X_t$, nói cách khác: $A_t=\pi(X_t)$.

Chính sách ngẫu nhiên:

Chính sách ngẫu nhiên là một ánh xạ xác suất, trong đó $\pi(\cdot|X_t): \mathcal{A}\rightarrow\mathbb{R}$ thể hiện rằng phân phối xác suất sẽ sinh ra hành động $A_t$.

Ta có thêm một khái niệm quan trọng khác, đó là chuỗi phần thưởng Markov (Markov reward process - MRP). Khi nhắc tới khái niệm này, ta sẽ xem xét một chuỗi MDP cùng với một chính sách. Gọi chính sách ta đang xem xét là $\pi$ và $\mathcal{M} = (\mathcal{X}, \mathcal{A}, \mathcal{P})$. Khi đó, phân phối xác suất chuyển trạng thái của MRP là $\mathcal{P}^{\pi}$. So sánh một chút, ta có phân phối xác suất chuyển trạng thái của MDP là $\mathcal{P}$, còn của MRP là $\mathcal{P}^{\pi}$. Ta có mối quan hệ như sau:

\[\mathcal{P}^{\pi}(\cdot \| x) = \sum_{a\in\mathcal{A}}\pi(a \| x)\mathcal{P}(\cdot \| x, a)\]

Một cách tương tự với $V^{\ast}$, ta định nghĩa hàm giá trị $V^{\pi}: \mathcal{X}\rightarrow\mathbb{R}$ là tổng phần thưởng kỳ vọng suy biến dưới cơ chế chọn hành động là $\pi$, nói cách khác:

\[V^{\pi}(x) = \mathbb{E}[ \sum_{t=0}^{+\infty}\gamma^t R_{t+1} \| X_0 = x]\]

Ý nghĩa của $V^{\pi}$ là cho biết giá trị tổng phần thưởng kỳ vọng suy biến nếu các hành động được chọn trong chuỗi MDP tuân theo chính sách $\pi$. So sánh với $V^{\ast}$, ta thấy rằng: $V^{\ast}$ là giá trị tối ưu của tất cả các chính sách, còn $V^{\pi}$ chỉ đơn giản là giá trị theo một chính sách; chính vì vậy, hàm $V^{\pi}$ còn được gọi là hàm giá trị. Trong định nghĩa trên, ở vế điều kiện của xác suất, $X_0$ thể hiện rằng, ta sẽ coi trạng thái tại thời điểm hiện tại là thời điểm đầu tiên và tính tổng phần thưởng kỳ vọng tại bắt đầu từ bước đó.

Hàm hành động-giá trị (action-value function)

Hàm giá trị đôi khi là chưa đủ để có thể đánh giá chi tiết từng hành động tại mỗi thời điểm. $ V^{\pi}(x)$ chỉ cho ta biết giá trị tại từng trạng thái, ta không thể quan sát được giá trị của một hành động $a$ nếu thực hiện ở trạng thái $x$ sẽ ảnh hưởng như nào, vì lẽ đó, người ta đưa thêm một khái niệm khác cũng không kém phần quan trọng:

\[Q^{\pi}(x, a) = \mathbb{E}[ \sum_{t=0}^{+\infty}\gamma^t R_{t+1} \| X_0 = x, A_0=a]\]

$ Q^{\pi}$ là ánh xạ: $Q^{\pi}: \mathcal{X}\times\mathcal{A}\rightarrow\mathbb{R}$ thể hiện giá trị tương ứng tại trạng thái $x$ nếu ta lựa chọn hành động $a$. Tương tự với $V^{\ast}$, ta cũng có $Q^{\ast}$ là giá trị tối ưu của tất cả các chính sách. Như vậy, tới đây, bài viết cũng đã giới thiệu toàn bộ các kiến thức cơ bản nhất liên quan đến MDP và ngay sau đây là một số định nghĩa, định lý mà các nhà toán học đã chứng minh được.

Ta có các mối quan hệ giữa $Q^{\ast}$ và $V^{\ast}$ như sau:

\[V^{\ast} = \sup_{a\in\mathcal{A}}Q^{\ast}(x, a)\] \[Q^{\ast}(x, a) = r(x, a) + \gamma\times\sum_{y\in\mathcal{X}}\mathcal{P}(y,R \| x, a)\times V^{\ast}(y)\] \[\sum_{a\in\mathcal{A}}\pi(a \| x)Q^{\ast}(x, a) = V^{\ast}(x)\]

Phương trình Bellman cho chính sách cố định: Nếu $\pi$ là một chính sách cố định thì ta có:

\[V^{\pi}(x) = r(x, \pi(x)) + \gamma\times\sum_{y\in\mathcal{X}}\mathcal{P}(y,R \| x, \pi(x))\times V^{\pi}(y), \forall x\in\mathcal{X}\]

Dựa vào phương trình Bellman, chúng ta có thể tính hàm giá trị $V^{\pi}$ bằng phương pháp quy hoạch động, chính vì vậy, ban đầu các mô hình MDP hay được giải quyết theo phương pháp này. Chúng ta sẽ được gặp lại phương trình Bellman này ở các bài tiếp theo.

Phương trình Bellman cho chính sách tối ưu:

\[V^{\ast}(x) = \sup_{a\in\mathcal{A}}\{r(x, a) + \gamma\times\sum_{y\in\mathcal{X}}\mathcal{P}(y,R \| x, a)\times V^{\ast}(y)\}, \forall x\in\mathcal{X}\]