Trong bài viết này, mình sẽ trình bày các khái niệm về Reinforcement Learning. Vì mình là một người thích dùng tiếng Việt khi trình bày về các kiến thức nên mình sẽ thống nhất tên gọi mình sẽ dùng trong suốt blog là Học tăng cường.

Giới thiệu về bài toán trong học tăng cường

Nhắc tới học tăng cường, ta đang nhắc tới cả một bài toán trong lĩnh vực học máy và cả một mảng nghiên cứu rất lâu đời của học máy.

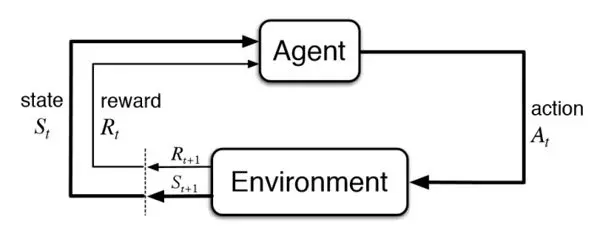
Hình 1: Minh họa về Học tăng cường

Một bài toán trong học tăng cường thường có mô thức được minh họa ở hình 1. Trong bài toán này, chúng ta có một tác tử (agent) tương tác với một môi trường (environment). Quá trình tương tác này có thể hiểu đơn giản như sau: tại thời điểm nhất định $\boldsymbol{t}$, tác tử lựa chọn hành động $A_t$ tương tác tới môi trường, môi trường sau khi nhận hành động này của tác tử có thể biểu hiện ra bên ngoài và bằng cơ chế quan sát (perceive) của mình, tác tử sẽ biết được trạng thái môi trường vừa được chuyển dịch (transition) sau hành động của nó từ $S_\boldsymbol{t}$ sang $S_\boldsymbol{t+1}$, cũng như phần thưởng (reward) $R_\boldsymbol{t+1}$. Ta có thể hiểu nôm na phần thưởng như một độ đo để cho tác tử biết rằng hành động nó vừa thực hiện tốt hay xấu và tốt hay xấu như thế nào. Bài toán học tăng cường được phát biểu rất đơn giản: Làm thể nào để có thể điều khiển được một tác tử để phần thưởng mà nó thu được là lớn nhất?

Thông thường, các bài toán nghiên cứu về Học tăng cường giả sử môi trường mà tác tử tương tác là môi trường ngẫu nhiên (stochastic) và khả năng quan sát của tác tử là đủ chi tiết để nó có thể thu thập đủ tốt dữ liệu từ môi trường.

Lược sử về các phương pháp giải quyết bài toán MDP

Một trong những cách hiệu quả nhất để mô hình bài toán Học tăng cường đó là sử dụng mô hình chuỗi đưa ra quyết định Markov (Markovian Decision Process). Mô hình này sẽ được trình bày ở bài sau và vẫn được coi là chuẩn để mô hình hóa các bài toán Học tăng cường. Thuở ban đầu, phương pháp được coi là chính tắc để giải các bài toán MDP là sử dụng quy hoạch động (Bellman, 1957). Tuy nhiên phương pháp giải này chỉ có thể giải trong trường hợp tập trạng thái và tập hành động là rất nhỏ, đối với các bài toán mà tập không gian trạng thái, hành động lớn hơn (các bài toán thực tế trong robotics có chiều không gian hành động lên đến 12) thì quy hoạch động tỏ ra không khả thi (infeasible).

Dù quy hoạch động vẫn được nghiên cứu và có nhiều kết quả trong lý thuyết Học tăng cường hiện đại (Putterman, 1994; Bertsekas, 2005, 2012) nhưng ngày nay, các thuật toán quy hoạch động thường được chuyển thành các ý tưởng để có thể giải MDP hiệu quả hơn. Để giải MDP hiệu quả hơn, có hai ý tưởng tổng quát hơn, và cũng là những câu hỏi vĩ mô mà Học tăng cường xem xét: Ý tưởng đầu tiên là giải quyết bài toán điều khiển (control problem), có thể hiểu đơn giản là: Làm thể nào để chúng ta có thể đưa ra những quyết định hiệu quả với một bài toán cho trước?; Ý tưởng tiếp theo là giải quyết bài toán dự đoán giá trị (value prediction) bằng các phương pháp xấp xỉ, ta có thể tạm hiểu bài toán thứ hai như là: Với một chính sách cho trước gán với một bài toán, làm thế nào để có thể đánh giá được chính sách đó? Ngày nay, thuật ngữ được sử dụng phổ biến hơn cho các thuật toán quy hoạch động trong MDP là xấp xỉ quy hoạch động (approximate dynamic programming).

Thời hiện đại của lĩnh vực Học tăng cường đã chứng kiến rất nhiều thành công, có thể kể đến như AlphaZero (DeepMind 2017), mô hình chơi các trò chơi Atari được huấn luyện bởi Deep Reinforcement Learning của Mnih et al năm 2015 đã tạo một tiếng vang lớn với cộng đồng các nhà nghiên cứu Học máy. Bot huấn luyện bởi OpenAI bằng phương pháp học tăng cường chiến thắng 1v1 người chơi top trong trò chơi nổi tiếng Dota2. Bot trò chơi Super Smash Brothers Melee chiến thắng người chơi chuyên nghiệp trong 1v1 tại Falcon dittos. (Firoiu et al, 2017)…

Một số cặp khái niệm quan trọng trong Học tăng cường

Trong học tăng cường, có rất nhiều cặp khái niệm đi cặp với nhau, một số tương phản nhau, một số thì bổ sung ý nghĩa cho nhau, các cặp khái niệm trình bày ngay trong chương này thì có thể người đọc chưa làm quen với Học tăng cường không hiểu được ngay nhưng xuyên suốt blog này, các khái niệm này sẽ được nhắc lại, vì vậy, nếu người đọc lúc này chưa quen với các khái niệm này thì có thể tạm ghi nhớ tên gọi của nó để về sau sẽ được phân tích chi tiết hơn.

Exploitation vs. Exploration

Trong Học tăng cường, tận dụng (exploitation) và khai phá (exploration) là hai thành phần không thể thiếu của bất kỳ giải thuật học tăng cường nào. Giả sử như tác tử của chúng ta muốn đưa ra quyết định hiệu quả, thì nó phải thực hiện khai phá đủ để có thể biết được đặc trưng của các hành động. Khi đã khai phá xong và nhận biết được đặc trưng các hành động, tác tử phải tiến hành tận dụng những đặc trưng khai thác được để đưa ra hành động có phần thưởng lớn nhất.

On-policy vs. Off-policy

Trong các bài toán điều khiển, tác tử sẽ đưa ra quyết định tuân theo một chính sách hành vi (behavior policy) và nó học một chính sách mục tiêu (target policy). Nếu như chính sách mục tiêu khác với chính sách hành vi, nó được gọi là off-policy, còn ngược lại, được coi là on-policy.

Model-based vs. Model-free

Khái niệm này xuất hiện trong cả bài toán dự đoán và bài toán điều khiển. Nếu thuật toán mà chúng ta xây dựng học biểu diễn môi trường, thì thuật toán đó được coi là Model-based, ngược lại, nếu thuật toán không học biểu diễn môi trường, thì thuật toán được coi là Model-free.

Value-based vs. Policy-based

Value-based là các giải thuật dựa vào học dự đoán giá trị, còn policy-based là các giải thuật dựa vào một chính sách.

Sơ khảo các kiến thức liên quan

Như thường lệ, ta gọi $\mathbb{N}={0,1,2\dots}$ là tập số tự nhiên, $\mathbb{R}$ là tập số thực.
Một vector $u\in\mathbb{R}^d$ là đại lượng có hướng, được biểu diễn bởi $(u_1, u_2, \dots, u_d)$, mỗi $u_i, 1\leq i\leq d$ thường được gọi là một thành phần (feature). Tích vô hướng giữa hai vector $u, v\in\mathbb{R}^d$ là $\langle u, v\rangle = \sum_{i=1}^d u_iv_i$.
Một số các chuẩn trong không gian metric quen thuộc như: L2: $| u| = \langle u, u\rangle$, L1: $| u| = \max_{i=1,2,\dots, d}|u_i|$.
Đối với một hàm $v$ phụ thuộc vào $\theta$, giả sử: $v = v(\theta, x)$. Khi đó, đạo hàm riêng của $v$ theo $\theta$ được ký hiệu là: $\frac{\partial v}{\partial \theta}$. Đạo hàm toàn phần của $v$ theo $\theta$ được ký hiệu là $\nabla_{\theta} v = \frac{dv}{d\theta}$.
Giả sử $P$ là một phân phối xác suất nào đó. Nếu biến ngẫu nhiên $X$ được sinh ra bằng cách chọn mẫu dựa trên phân phối $P$, ta viết là: $X{\sim}P$.

Sơ lược về các bài viết của blog

Blog này có thể hiểu sẽ được chia làm 3 phần: Phần đầu giới thiệu về các khái niệm cơ bản nhất của Học tăng cường, phần hai giới thiệu về bài toán dự đoán giá trị và các giải thuật để giải quyết bài toán này, phần cuối cùng giới thiệu về bài toán điều khiển cũng như các giải thuật liên quan.